
Well, we’re finally at the point in this GSoC project where the end is glimmering on the horizon. I have completed the Held Karp relaxation, generating a spanning tree distribution and now sampling from that distribution. That means that it is time to start thinking about how to link these separate components into one algorithm.
Recall that from the Asadpour paper the overview of the algorithm is
Algorithm 1 An $O(\log n / \log \log n)$-approximation algorithm for the ATSP
Input: A set $V$ consisting of $n$ points and a cost function $c\ :\ V \times V \rightarrow \mathbb{R}^+$ satisfying the triangle inequality.
Output: $O(\log n / \log \log n)$-approximation of the asymmetric traveling salesman problem instance described by $V$ and $c$.
- Solve the Held-Karp LP relaxation of the ATSP instance to get an optimum extreme point solution $x^*$. Define $z^*$ as in (5), making it a symmetrized and scaled down version of $x^*$. Vector $z^*$ can be viewed as a point in the spanning tree polytope of the undirected graph on the support of $x^*$ that one obtains after disregarding the directions of arcs (See Section 3.)
- Let $E$ be the support graph of $z^*$ when the direction of the arcs are disregarded. Find weights ${\tilde{\gamma}}_{e \in E}$ such that the exponential distribution on the spanning trees, $\tilde{p}(T) \propto \exp(\sum_{e \in T} \tilde{\gamma}_e)$ (approximately) preserves the marginals imposed by $z^*$, i.e. for any edge $e \in E$,
$\sum\_{T \in \mathcal{T} : T \ni e} \tilde{p}(T) \leq (1 + \epsilon) z^\*\_e$, for a small enough value of $\epsilon$. (In this paper we show that $\epsilon = 0.2$ suffices for our purpose. See Section 7 and 8 for a description of how to compute such a distribution.)- Sample $2\lceil \log n \rceil$ spanning trees $T_1, \dots, T_{2\lceil \log n \rceil}$ from $\tilde{p}(.)$. For each of these trees, orient all its edges so as to minimize its cost with respect to our (asymmetric) cost function $c$. Let $T^*$ be the tree whose resulting cost is minimal among all of the sampled trees.
- Find a minimum cost integral circulation that contains the oriented tree $\vec{T}^*$. Shortcut this circulation to a tour and output it. (See Section 4.)
We are now firmly in the steps 3 and 4 area.
Going all the way back to my post on 24 May 2021 titled Networkx Function stubs the only function left is asadpour_tsp, the main function which needs to accomplish this entire algorithm.
But before we get to creating pseudo code for it there is still step 4 which needs a thorough examination.
Circulation and Shortcutting#
Once we have sampled enough spanning trees from the graph and converted the minimum one into $\vec{T}^*$ we need to find the minimum cost integral circulation in the graph which contains $\vec{T}^*$.
While NetworkX a minimum cost circulation function, namely, min_cost_flow, it is not suitable for the Asadpour algorithm out of the box.
The problem here is that we do not have node demands, we have edge demands.
However, after some reading and discussion with one of my mentors Dan, we can convert the current problem into one which can be solved using the min_cost_flow function.
The problem that we are trying to solve is called the minimum cost circulation problem and the one which min_cost_flow is able to solve is the, well, minimum cost flow problem.
As it happens, these are equivalent problems, so I can convert the minimum cost circulation into a minimum cost flow problem by transforming the minimum edge demands into node demands.
Recall that at this point we have a directed minimum sampled spanning tree $\vec{T}^*$ and that the flow through each of the edges in $\vec{T}^*$ needs to be at least one. From the perspective of a flow problem, $\vec{T}^*$ is moving some flow around the graph. However, in order to augment $\vec{T}^*$ into an Eulerian graph so that we can walk it, we need to counteract this flow so that the net flow for each node is 0 $(f(\delta^+(v)) = f(\delta^-(v))$ in the Asadpour paper).
So, we find the net flow of each node and then assign its demand to be the negative of that number so that the flow will balance at the node in question. If the total flow at any node $i$ is $\delta^+(i) - \delta^-(i)$ then the demand we assign to that node is $\delta^-(i) - \delta^+(i)$. Once we assign the demands to the nodes we can temporarily ignore the edge lower capacities to find the minimum flow.
For more information on the conversion process, please see [2].
After the minimum flow is found, we take the support of the flow and add it to the $\vec{T}^*$ to create a multigraph $H$.
Now we know that $H$ is weakly connected (it contains $\vec{T^*}$) and that it is Eulerian because for every node the in-degree is equal to the out-degree.
A closed eulerian walk or eulerian circuit can be found in this graph with eulerian_circuit.
Here is an example of this process on a simple graph. I suspect that the flow will not always be the back edges from the spanning tree and that the only reason that is the case here is due to the small number of vertcies.
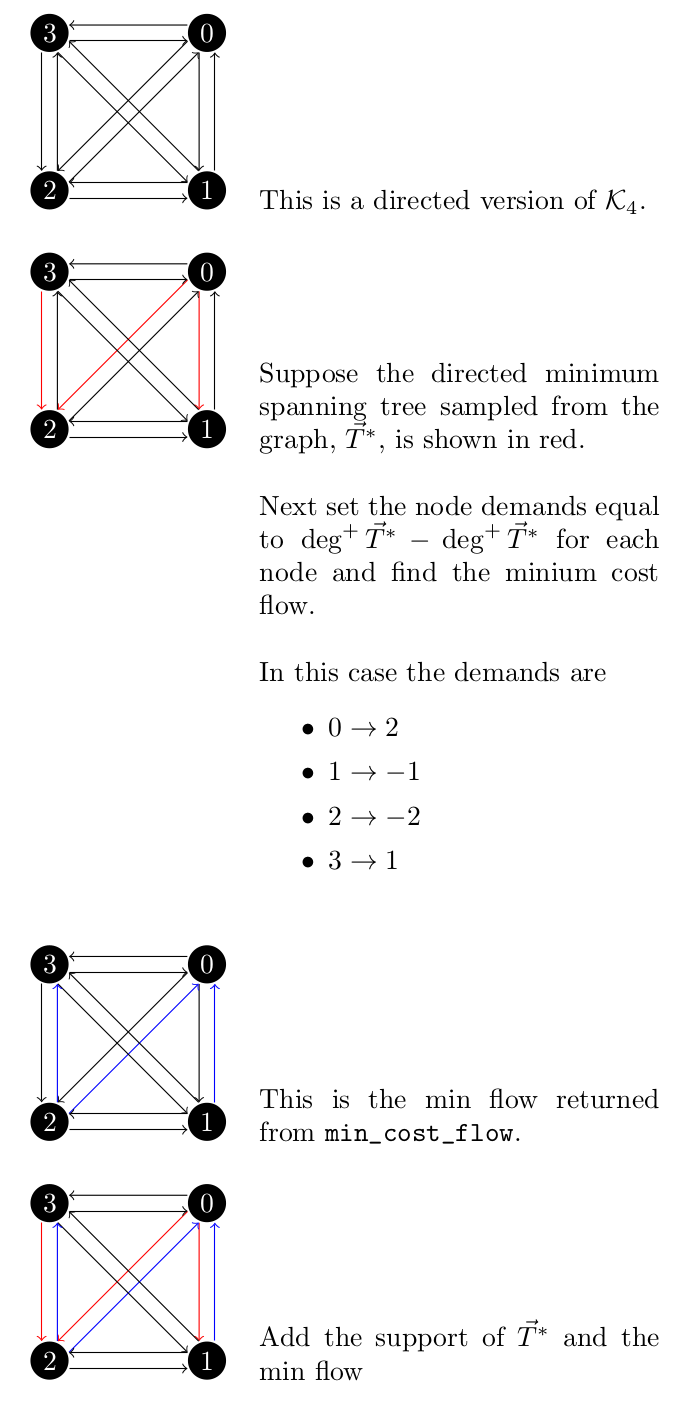
Finally, we take the eulerian circuit and shortcut it.
On the plus side, the shortcutting process is the same as the Christofides algorithm so that is already the _shortcutting helper function in the traveling salesman file.
This is really where it is critical that the triangle inequality holds so that the shortcutting cannot increase the cost of the circulation.
Pseudo code for asadpour_tsp#
Let’s start with the function signature.
def asadpour_tsp
Input: A complete graph G with weight being the attribute key for the edge weights.
Output: A list of edges which form the approximate ATSP solution.
This is exactly what we’d expect, take a complete graph $G$ satisfying the triangle inequality and return the edges in the approximate solution to the asymmetric traveling salesman problem.
Recall from my post Networkx Function Stubs what the primary traveling salesman function, traveling_salesman_problem will ensure that we are given a complete graph that follows the triangle inequality by using all-pairs shortest path calculations and will handle if we are expected to return a true cycle or only a path.
The first step in the Asadpour algorithm is the Held Karp relaxation. I am planning on editing the flow of the algorithm here a bit. If the Held Karp relaxation finds an integer solution, then we know that is one of the optimal TSP routes so there is no point in continuing the algorithm: we can just return that as an optimal solution. However, if the Held Karp relaxation finds a fractional solution we will press on with the algorithm.
z_star = held_karp(G)
# test to see if z_star is a graph or dict
if type(z_star) is nx.DiGraph
return z_star.edges
Once we have the Held Karp solution, we create the undirected support of z_star for the next step of creating the exponential distribution of spanning trees.
z_support = nx.MultiGraph()
for u, v in z_star
if not in z_support.edges
edge_weight = min(G[u][v][weight], G[v][u][weight])
z_support.add_edge(u, v, weight=edge_weight)
gamma = spanning_tree_distribution(z_support, z_star)
This completes steps 1 and 2 in the Asadpour overview at the top of this post. Next we sample $2 \lceil \log n \rceil$ spanning trees.
for u, v in z_support.edges
z_support[u][v][lambda] = exp(gamma[(u, v)])
for _ in range 1 to 2 ceil(log(n))
sampled_tree = sample_spanning_tree(G)
sampled_tree_weight = sampled_tree.size()
if sampled_tree_weight < minimum_sampled_tree_weight
minimum_sampled_tree = sampled_tree.copy()
minimum_sampled_tree_weight = sampled_tree_weight
Now that we have the minimum sampled tree, we need to orient the edge directions to keep the cost equal to that minimum tree.
We can do this by iterating over the edges in minimum_sampled_tree and checking the edge weights in the original graph $G$.
Using $G$ is required here if we did not record the minimum direction which is a possibility when we create z_support.
t_star = nx.DiGraph
for u, v, d in minimum_sampled_tree.edges(data=weight)
if d == G[u][v][weight]
t_star.add_edge(u, v, weight=d)
else
t_star.add_edge(v, u, weight=d)
Next we create a mapping of nodes to node demands for the minimum cost flow problem which was discussed earlier in this post.
I think that using a dict is the best option as it can be passed into set_node_attributes all at once before finding the minimum cost flow.
for n in t_star
node_demands[n] = t_star.out_degree(n) - t_star.in_degree(n)
nx.set_node_attributes(G, node_demands)
flow_dict = nx.min_cost_flow(G)
Take the Eulerian circuit and shortcut it on the way out.
Here we can add the support of the flow directly to t_star to simulate adding the two graphs together.
for u, v in flow_dict
if edge not in t_star.edges and flow_dict[u, v] > 0
t_star.add_edge(u, v)
eulerian_curcuit = nx.eulerian_circuit(t_star)
return _shortcutting(eulerian_curcuit)
That should be it.
Once the code for asadpour_tsp is written it will need to be tested.
I’m not sure how I’m going to create the test cases yet, but I do plan on testing it using real world airline ticket prices as that is my go to example for the asymmetric traveling salesman problem.
References#
A. Asadpour, M. X. Goemans, A. Mardry, S. O. Ghran, and A. Saberi, An o(log n / log log n)-approximation algorithm for the asymmetric traveling salesman problem, Operations Research, 65 (2017), pp. 1043-1061.
D. Williamson, ORIE 633 Network Flows Lecture 11, 11 Oct 2007, https://people.orie.cornell.edu/dpw/orie633/LectureNotes/lecture11.pdf.