Looking for a new method to solve the Held-Karp relaxation from the original Held and Karp paperAfter talking with my GSoC mentors about what we all believe to be the most difficult part of the Asadpour algorithm, the Held-Karp relaxation, we came to several conclusions:
- The Asadpour paper recommends using the ellipsoid method so that their algorithm runs in polynomial time.
We do not need a polynomial time, just an algorithm with reasonable execution time.
An example of this would be the ellipsoid algorithm versus the simplex algorithm.
While the simplex algorithm is exponential, in practice it is almost always faster than the ellipsoid algorithm.
- Our interest in the ellipsoid algorithm was not based on performance, but rather the ability for the ellipsoid algorithm to be able to handle a linear program with an exponential number of constraints.
This was done with a separation oracle, see my post here for more information about the oracle.
- Implementing a robust ellipsoid algorithm solver (something notable missing from the scientific python ecosystem) was a GSoC project onto itself and beyond the scope of this project for NetworkX.
Thus, alternative methods for solving the Held-Karp relaxation needed to be investigated.
To this end, we turned to the original 1970 paper by Held and Karp, The Traveling Salesman Problem and Minimum Spanning Trees to see how they proposed solving the relaxation (Note that this paper was published before the ellipsoid algorithm was applied to linear programming in 1979).
The Held and Karp paper discusses three methods for solving the relaxation:
- Column Generating: An older method of solving very large linear programs where only the variables that influence the optimal solution need to be examined.
- Ascent Method: A method based around maximizing the dual of the linear program which is best described as seeking the direction of ascent for the objective function in a similar way to the notion of a gradient in multivariate calculus.
- Branch and Bound: This method has the most theoretical benefits and seeks to augment the ascent method to avoid the introduction of fractional weights which are the largest contributors to a slow convergence rate.
But before we explore the methods that Held and Karp discuss, we need to ensure that these methods still apply to solving the Held-Karp relaxation within the context of the Asadpour paper.
The definition of the Held-Karp relaxation that I have been using on this blog comes from the Asadpour paper, section 3 and is listed below.
$$
\begin{array}{c l l}
\text{min} & \sum_{a} c(a)x_a \\\
\text{s.t.} & x(\delta^+(U)) \geqslant 1 & \forall\ U \subset V \text{ and } U \not= \emptyset \\\
& x(\delta^+(v)) = x(\delta^-(v)) = 1 & \forall\ v \in V \\\
& x_a \geqslant 0 & \forall\ a
\end{array}
$$
The closest match to this program in the Held Karp paper is their linear program 3, which is a linear programming representation of the entire traveling salesman problem, not solely the relaxed version.
Note that Held and Karp were dealing with the symmetric TSP (STSP) while Asadpour is addressing the asymmetric or directed TSP (ATSP).
$$
\begin{array}{c l l}
\text{min} & \sum_{1 \leq i < j \leq n} c_{i j}x_{i j} \\\
\text{s.t.} & \sum_{j > i} x_{i j} + \sum_{j < i} x_{j i} = 2 & (i = 1, 2, \dots, n) \\\
& \sum_{i \in S\\\ j \in S\\\ i < j} x_{i j} \leq |S| - 1 & \text{for any proper subset } S \subset {2, 3, \dots, n} \\\
& 0 \leq x_{i j} \leq 1 & (1 \leq i < j \leq n) \\\
& x_{i j} \text{integer} \\\
\end{array}
$$
The last two constraints on the second linear program is correctly bounded and fits within the scope of the original problem while the first two constraints do most of the work in finding a TSP tour.
Additionally, changing the last two constraints to be $x_{i j} \geq 0$ is the Held Karp relaxation.
The first constraint, $\sum_{j > i} x_{i j} + \sum_{j < i} x_{j i} = 2$, ensures that for every vertex in the resulting tour there is one edge to get there and one edge to leave by.
This matches the second constraint in the Asadpour ATSP relaxation.
The second constraint in the Held Karp formulation is another form of the subtour elimination constraint seen in the Asadpour linear program.
Held and Karp also state that
In this section, we show that minimizing the gap $f(\pi)$ is equivalent to solving this program without the integer constraints.
on page 1141, so it would appear that solving one of the equivalent programs that Held and Karp forumalate should work here.
Column Generation Technique
The Column Generation technique seeks to solve linear program 2 from the Held and Karp paper, stated as
$$
\begin{array}{c l}
\text{min} & \sum_{k} c_ky_k \\\
\text{s.t.} & y_k \geq 0 \\\
& \sum_k y_k = 1 \\\
& \sum_{i = 2}^{n - 1} (-v_{i k})y_k = 0 \\\
\end{array}
$$
Where $v_{i k}$ is the degree of vertex $i$ in 1-Tree $k$ minus two, or $v_{i k} = d_{i k} - 2$ and each variable $y_k$ corresponds to a 1-Tree $T^k$.
The associated cost $c_k$ for each tree is the weight of $T^k$.
The rest of this method uses a simplex algorithm to solve the linear program.
We only focus on the edges which are in each of the 1-Trees, giving each column the form
$$
\begin{bmatrix}
1 & -v_{2k} & -v_{3k} & \dots & -v_{n-1,k}
\end{bmatrix}^T
$$
and the column which enters the solution in the 1-Tree for which $c_k + \theta + \sum_{j=2}^{n-1} \pi_jv_{j k}$ is a minimum where $\theta$ and $\pi_j$ come from the vector of ‘shadow prices’ given by $(\theta, \pi_2, \pi_3, \dots, \pi_{n-1})$.
Now the basis is $(n - 1) \times (n - 1)$ and we can find the 1-Tree to add to the basis using a minimum 1-Tree algorithm which Held and Karp say can be done in $O(n^2)$ steps.
I am already familiar with the simplex method, so I will not detail it’s implementation here.
This technique is slow to converge.
Held and Karp programmed in on an IBM/360 and where able to solve problems consestinal for up to $n = 12$.
Now, on a modern computer the clock rate is somewhere between 210 and 101,500 times faster (depending on the model of IBM/360 used), so we expect better performance, but cannot say at this time how much of an improvement.
They also talk about a heuristic procedure in which a vertex is eliminated from the program whenever the choice of its adjacent vertices was ’evident’.
Technical details for the heuristic where essentially non-existent, but
The procedure showed promise on examples up to $n = 48$, but was not explored systematically
Ascent Method
This paper from Held and Karp is about minimizing $f(\pi)$ where $f(\pi)$ is the gap between the permuted 1-Trees and a TSP tour.
One way to do this is to maximize the dual of $f(\pi)$ which is written as $\text{max}_{\pi}\ w(\pi)$ where
$$
w(\pi) = \text{min}_k\ (c_k + \sum_{i=1}^{i=n} \pi_iv_{i k})
$$
This method uses the set of indices of 1-Trees that are of minimum weight with respect to the weights $\overline{c}_{i j} = c_{i j} + \pi_i + \pi_j$.
$$
K(\pi) = {k\ |\ w(\pi) = c_k + \sum_{i=1}^{i=n} \pi_i v_{i k}}
$$
If $\pi$ is not a maximum point of $w$, then there will be a vector $d$ called the direction of ascent at $\pi$.
This is theorem 3 and a proof is given on page 1148.
Let the functions $\Delta(\pi, d)$ and $K(\pi, d)$ be defined as below.
$$
\Delta(\pi, d) = \text{min}_{k \in K(\pi)}\ \sum_{i=1}^{i=n} d_iv_{i k} \\\
K(\pi, d) = {k\ |\ k \in K(\pi) \text{ and } \sum_{i=1}^{i=n} d_iv_{i k} = \Delta(\pi, d)}
$$
Now for a sufficiently small $\epsilon$, $K(\pi + \epsilon d) = K(\pi, d)$ and $w(\pi + \epsilon d) = w(\pi) + \epsilon \Delta(\pi, d)$, or the value of $w(\pi)$ increases and the growth rate of the minimum 1-Trees is at its smallest so we maintain the low weight 1-Trees and progress farther towards the optimal value.
Finally, let $\epsilon(\pi, d)$ be the following quantity
$$
\epsilon(\pi, d) = \text{max}\ {\epsilon\ |\text{ for } \epsilon’ < \epsilon,\ K(\pi + \epsilon’d = K(\pi, d)}
$$
So in other words, $\epsilon(\pi, d)$ is the maximum distance in the direction of $d$ that we can travel to maintain the desired behavior.
If we can find $d$ and $\epsilon$ then we can set $\pi = \pi + \epsilon d$ and move to the next iteration of the ascent method.
Held and Karp did give a protocol for finding $d$ on page 1149.
- Set $d$ equal to the zero $n$-vector.
- Find a 1-tree $T^k$ such that $k \in K(\pi, d)$.
- If $\sum_{i=1}^{i=n} d_iv_{i k} > 0$ STOP.
- $d_i \leftarrow d_i + v_{i k},$ for $i = 2, 3, \dots, n$
- GO TO 2.
There are two things which must be refined about this procedure in order to make it implementable in Python.
- How do we find the 1-Tree mentioned in step 2?
- How do we know when there is no direction of ascent? (i.e. how do we know when we are at the maximal value of $w(\pi)$?)
Held and Karp have provided guidance on both of these points.
In section 6 on matroids, we are told to use a method developed by Dijkstra in A Note on Two Problems in Connexion with Graphs, but in this particular case that is not the most helpful.
I have found this document, but there is a function called minimum_spanning_arborescence already within NetworkX which we can use to create a minimum 1-Arborescence.
That process would be to find a minimum spanning arborescence on only the vertices in ${2, 3, \dots, n}$ and then connect vertex 1 to create the cycle.
In order to connect vertex 1, we would choose the outgoing arc with the smallest cost and the incoming arc with the smallest cost.
Finally, at the maximum value of $w(\pi)$, there is no direction of ascent and the procedure outlined by Held and Karp will not terminate.
Their article states on page 1149 that
Thus, when failure to terminate is suspected, it is necessary to check whether no direction of ascent exists; by the Minkowski-Farkas lemma this is equivalent to the existence of nonnegative coefficients $\alpha_k$ such that
$ \sum_{k \in K(\pi)} \alpha_kv_{i k} = 0, \quad i = 1, 2, \dots, n $
This can be checked by linear programming.
While it is nice that they gave that summation, the rest of the linear program would have been useful too.
The entire linear program would be written as follows
$$
\begin{array}{c l l}
\text{max} & \sum_k \alpha_k \\\
\text{s.t.} & \sum_{k \in K(\pi)} \alpha_k v_{i k} = 0 & \forall\ i \in {1, 2, \dots n} \\\
& \alpha_k \geq 0 & \forall\ k \\\
\end{array}
$$
This linear program is not in standard form, but it is not difficult to convert it.
First, change the maximization to a minimization by minimizing the negative.
$$
\begin{array}{c l l}
\text{min} & \sum_k -\alpha_k \\\
\text{s.t.} & \sum_{k \in K(\pi)} \alpha_k v_{i k} = 0 & \forall\ i \in {1, 2, \dots n} \\\
& \alpha_k \geq 0 & \forall\ k \\\
\end{array}
$$
While the constraint is not intuitively in standard form, a closer look reveals that it is.
Each column in the matrix form will be for one entry of $\alpha_k$, and each row will represent a different value of $i$, or a different vertex.
The one constraint is actually a collection of very similar one which could be written as
$$
\begin{array}{c l}
\text{min} & \sum_k -\alpha_k \\\
\text{s.t.} & \sum_{k \in K(\pi)} \alpha_k v_{1 k} = 0 \\\
& \sum_{k \in K(\pi)} \alpha_k v_{2 k} = 0 \\\
& \vdots \\\
& \sum_{k \in K(\pi)} \alpha_k v_{n k} = 0 \\\
& \alpha_k \geq 0 & \forall\ k \\\
\end{array}
$$
Because all of the summations must equal zero, no stack and surplus variables are required, so the constraint matrix for this program is $n \times k$.
The $n$ obviously has a linear growth rate, but I’m not sure how big to expect $k$ to become.
$k$ is the set of minimum 1-Trees, so I believe that it will be manageable.
This linear program can be solved using the built in linprog function in the SciPy library.
As an implementation note, to start with I would probably check the terminating condition every iteration, but eventually we can find a number of iterations it has to execute before it starts to check for the terminating condition to save computational power.
One possible difficulty with the terminating condition is that we need to run the linear program with data from every minimum 1-Trees or 1-Arborescences, which means that we need to be able to generate all of the minimum 1-Trees.
There does not seem to be an easy way to do this within NetworkX at the moment.
Looking through the tree algorithms here they seem exclusively focused on finding one minimum branching of the required type and not all of those branchings.
Now we have to find $\epsilon$.
Theorem 4 on page 1150 states that
Let $k$ be any element of $K(\pi, d)$, where $d$ is a direction of ascent at $\pi$.
Then
$\epsilon(\pi, d) = \text{min}{\epsilon\ |\text{ for some pair } (e, e’),\ e’ \text{ is a substitute for } e \text{ in } T^k \\\ \text{ and } e \text{ and } e’ \text{ cross over at } \epsilon }$
The first step then is to determine if $e$ and $e’$ are substitutes.
$e’$ is a substitute if for a 1-Tree $T^k$, $(T^k - {e}) \cup {e’}$ is also a 1-Tree.
The edges $e = {r, s}$ and $e’ = {i, j}$ cross over at $\epsilon$ if the pairs $(\overline{c}_{i j}, d_i + d_j)$ and $(\overline{c}_{r s}, d_r + d_s)$ are different but
$$
\overline{c}_{i j} + \epsilon(d_i + d_j) = \overline{c}_{r s} + \epsilon(d_r + d_s)
$$
From that equation, we can derive a formula for $\epsilon$.
$$
\begin{array}{r c l}
\overline{c}_{i j} + \epsilon(d_i + d_j) &=& \overline{c}_{r s} + \epsilon(d_r + d_s) \\\
\epsilon(d_i + d_j) &=& \overline{c}_{r s} + \epsilon(d_r + d_s) - \overline{c}_{i j} \\\
\epsilon(d_i + d_j) - \epsilon(d_r + d_s) &=& \overline{c}_{r s} - \overline{c}_{i j} \\\
\epsilon\left((d_i + d_j) - (d_r + d_s)\right) &=& \overline{c}_{r s} - \overline{c}_{i j} \\\
\epsilon(d_i + d_j - d_r - d_s) &=& \overline{c}_{r s} - \overline{c}_{i j} \\\
\epsilon &=& \displaystyle \frac{\overline{c}_{r s} - \overline{c}_{i j}}{d_i + d_j - d_r - d_s}
\end{array}
$$
So we can now find $epsilon$ for any two pairs of edges which are substitutes for each other, but we need to be able to find substitutes in the 1-Tree.
We know that $e’$ is a substitute for $e$ if and only if $e$ and $e’$ are both incident to vertex 1 or $e$ is in a cycle of $T^k \cup {e’}$ that does not pass through vertex 1.
In a more formal sense, we are trying to find edges in the same fundamental cycle as $e’$.
A fundamental cycle is created when any edge not in a spanning tree is added to that spanning tree.
Because the endpoints of this edge are connected by one, unique path this creates a unique cycle.
In order to find this cycle, we will take advantage of find_cycle within the NetworkX library.
Below is a pseudocode procedure that uses Theorem 4 to find $\epsilon(\pi, d)$ that I sketched out.
It is not well optimized, but will find $\epsilon(\pi, d)$.
# Input: An element k of K(pi, d), the vector pi and the vector d.
# Output: epsilon(pi, d) using Theorem 4 on page 1150.
for each edge e in the graph G
if e is in k:
continue
else:
add e to k
let v be the terminating end of e
c = find_cycle(k, v)
for each edge a in c not e:
if a[cost] = e[cost] and d[i] + d[j] = d[r] + d[s]:
continue
epsilon = (a[cost] - e[cost])/(d[i] + d[j] - d[r] - d[s])
min_epsilon = min(min_epsilon, epsilon)
remove e from k
return min_epsilon
The ascent method is also slow, but would be better on a modern computer.
When Held and Karp programmed it, they tested it on some small problems up to 25 vertices and while the time per iteration was small, the number of iterations grew quickly.
They do not comment on if this is a better method than the Column Generation technique, but do point up that they did not determine if this method always converges to a maximum point of $w(\pi)$.
Branch and Bound Method
After talking with my GSoC mentors, we believe that this is the best method we can implement for the Held-Karp relaxation as needed by the Asadpour algorithm.
The ascent method is embedded within this method, so the in depth exploration of the previous method is required to implement this one.
Most of the notation in this method is reused from the ascent method.
The branch and bound method utilizes the concept that a vertex can be out-of-kilter.
A vertex $i$ is out-of-kilter high if
$$
\forall\ k \in K(\pi),\ v_{i k} \geq 1
$$
Similarly, vertex $i$ is out-of-kilter low if
$$
\forall\ k \in K(\pi),\ v_{i k} = -1
$$
Remember that $v_{i k}$ is the degree of the vertex minus 2.
We know that all the vertices have a degree of at least one, otherwise the 1-Tree $T^k$ would not be connected.
An out-of-kilter high vertex has a degree of 3 or higher in every minimum 1-Tree and an out-of-kilter low vertex has a degree of only one in all of the minimum 1-Trees.
Our goal is a minimum 1-Tree where every vertex has a degree of 2.
If we know that a vertex is out-of-kilter in either direction, we know the direction of ascent and that direction is a unit vector.
Let $u_i$ be an $n$-dimensional unit vector with 1 in the $i$-th coordinate.
$u_i$ is the direction of ascent if vertex $i$ is out-of-kilter high and $-u_i$ is the direction of ascent if vertex $i$ is out-of-kilter low.
Corollaries 3 and 4 from page 1151 also show that finding $\epsilon(\pi, d)$ is simpler when a vertex is out-of-kilter as well.
Corollary 3. Assume vertex $i$ is out-of-kilter low and let $k$ be an element of $K(\pi, -u_i)$.
Then $\epsilon(\pi, -u_i) = \text{min} (\overline{c}_{i j} - \overline{c}_{r s})$ such that ${i, j}$ is a substitute for ${r, s}$ in $T^k$ and $i \not\in {r, s}$.
Corollary 4. Assume vertex $r$ is out-of-kilter high.
Then $\epsilon(\pi, u_r) = \text{min} (\overline{c}_{i j} - \overline{c}_{r s})$ such that ${i, j}$ is a substitute for ${r, s}$ in $T^k$ and $r \not\in {i, j}$.
These corollaries can be implemented with a modified version of the pseudocode listing above for finding $\epsilon$ in the ascent method section.
Once there are no more out-of-kilter vertices, the direction of ascent is not a unit vector and fractional weights are introduced.
This is the cause of a major slow down in the convergence of the ascent method to the optimal solution, so it should be avoided if possible.
Before we can discuss implementation details, there are still some more primaries to be reviewed.
Let $X$ and $Y$ be disjoint sets of edges in the graph.
Then let $\mathsf{T}(X, Y)$ denote the set of 1-Trees which include all edges in $X$ but none of the edges in $Y$.
Finally, define $w_{X, Y}(\pi)$ and $K_{X, Y}(\pi)$ as follows.
$$
w_{X, Y}(\pi) = \text{min}_{k \in \mathsf{T}(X, Y)} (c_k + \sum_{i=1}^{i=n} \pi_i v_{i k}) \\\
K_{X, Y}(\pi) = {k\ |\ c_k + \sum \pi_i v_{i k} = w_{X, Y}(\pi)}
$$
From these functions, a revised definition of out-of-kilter high and low arise, allowing a vertex to be out-of-kilter relative to $X$ and $Y$.
During the completion of the branch and bound method, the branches are tracking in a list where each entry has the following format.
$$[X, Y, \pi, w_{X, Y}(\pi)]$$
Where $X$ and $Y$ are the disjoint sets discussed earlier, $\pi$ is the vector we are using to perturb the edge weights and $w_{X, Y}(\pi)$ is the bound of the entry.
At each iteration of the method, we consider the list entry with the minimum bound and try to find an out-of-kilter vertex.
If we find one, we apply one iteration of the ascent method using the simplified unit vector as the direction of ascent.
Here we can take advantage of integral weights if they exist.
Perhaps the documentation for the Asadpour implementation in NetworkX should state that integral edge weights will perform better but that claim will have to be supported by our testing.
If there is not an out-of-kilter vertex, we still need to find the direction of ascent in order to determine if we are at the maximum of $w(\pi)$.
If the direction of ascent exists, we branch.
If there is no direction of ascent, we search for a tour among $K_{X, Y}(\pi)$ and if none is found, we also branch.
The branching process is as follows.
From entry $[X, Y, \pi, w_{X, Y}(\pi)]$ an edge $e \not\in X \cup Y$ is chosen (Held and Karp do not give any criteria to branch on, so I believe the choose can be arbitrary) and the parent entry is replaced with two other entries of the forms
$$
[X \cup {e}, Y^*, \pi, w_{X \cup {e}, Y^*}(\pi)] \quad \text{and} \quad [X^*, Y \cup {e}, \pi, w_{X^*, Y \cup {e}}(\pi)]
$$
An example of the branch and bound method is given on pages 1153 through 1156 in the Held and Karp paper.
In order to implement this method, we need to be able to determine in addition to modifying some of the details of the ascent method.
- If a vertex is either out-of-kilter in either direction with respect to $X$ and $Y$.
- Search $K_{X, Y}(\pi)$ for a tour.
The Held and Karp paper states that in order to find an out-of-kilter vertex, all we need to do is test the unit vectors.
If for arbitrary member $k$ of $K(\pi, u_i)$, $v_{i k} \geq 1$ and the appropriate inverse holds for out-of-kilter low.
From this process we can find out-of-kilter vertices by sequentially checking the $u_i$’s in an $O(n^2)$ procedure.
Searching $K_{X, Y}(\pi)$ for a tour would be easy if we can enumerate that set minimum 1-Trees.
While I know how find one of the minimum 1-Trees, or a member of $K(\pi)$, I am not sure how to find elements in $K(\pi, d)$ or even all of the members of $K(\pi)$.
Using the properties in the Held and Karp paper, I do know how to refine $K(\pi)$ into $K(\pi, d)$ and $K(\pi)$ into $K_{X, Y}(\pi)$.
This will have to a blog post for another time.
The most promising research paper I have been able to find on this problem is this 2005 paper by Sörensen and Janssens titled An Algorithm to Generate all Spanning Trees of a Graph in Order of Increasing Cost.
From here we generate spanning trees or arborescences until the cost moves upward at which point we have found all elements of $K(\pi)$.
Held and Karp did not program this method.
We have some reason to believe that the performance of this method will be the best due to the fact that it is designed to be an improvement over the ascent method which was tested (somewhat) until $n = 25$ which is still better than the column generation technique which was only consistently able to solve up to $n = 12$.
References
A. Asadpour, M. X. Goemans, A. Mardry, S. O. Ghran, and A. Saberi, An o(log n / log log n)-approximation algorithm for the asymmetric traveling salesman problem, Operations Research, 65 (2017), pp. 1043-1061, https://homes.cs.washington.edu/~shayan/atsp.pdf.
Held, M., Karp, R.M. The traveling-salesman problem and minimum spanning trees. Operations research, 1970-11-01, Vol.18 (6), p.1138-1162. https://www.jstor.org/stable/169411
]]>















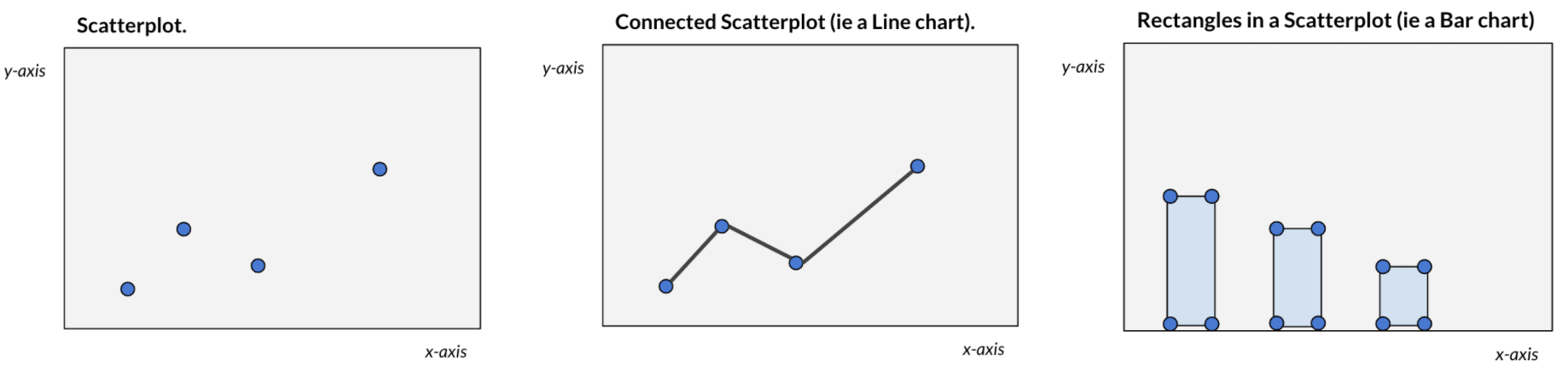
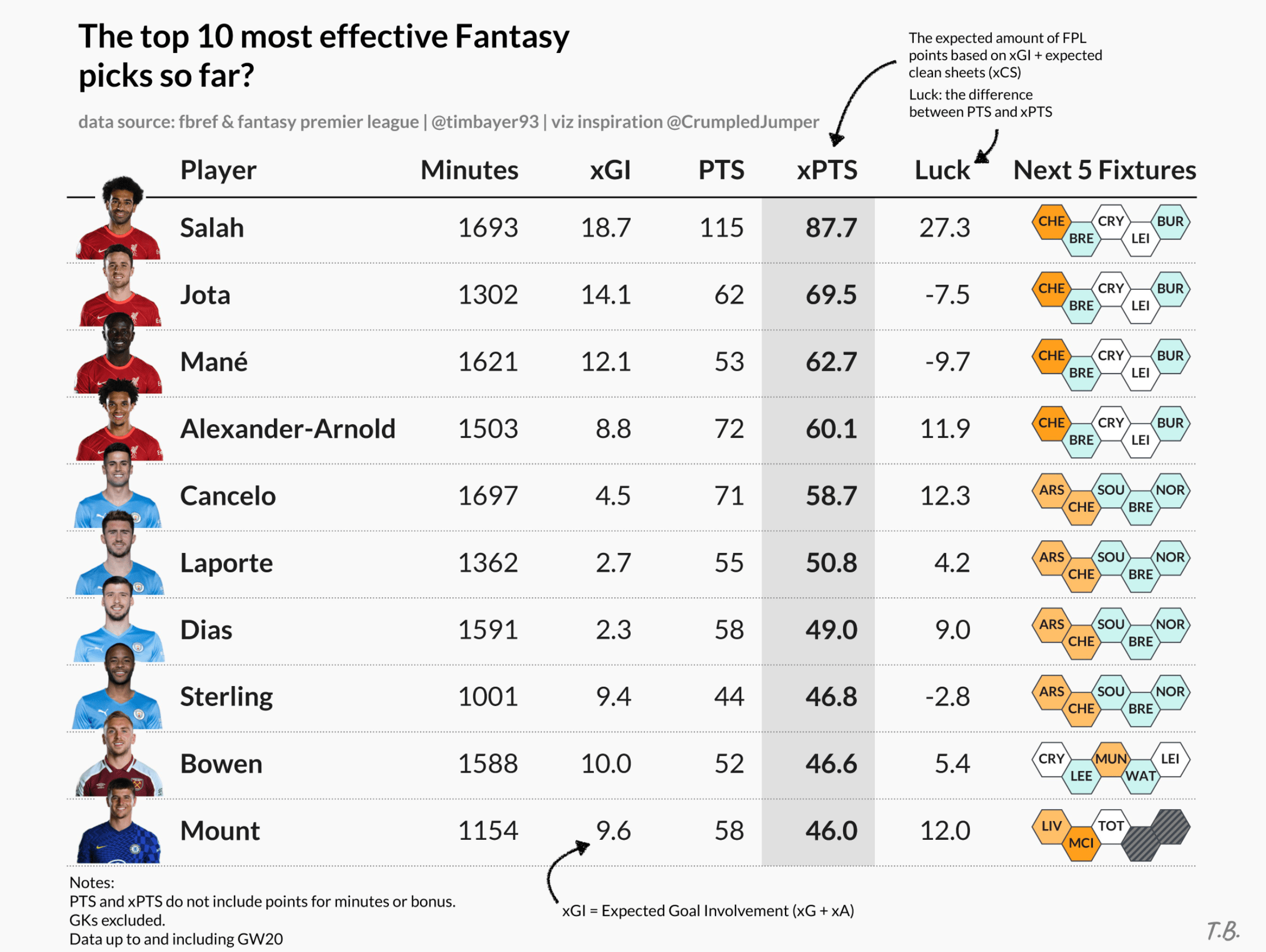



 First PR (left), Second PR (right)
First PR (left), Second PR (right)
 Font-Fallback Algorithm
Font-Fallback Algorithm
 Consider contributing to Matplotlib (Open Source in general) ❤️
Consider contributing to Matplotlib (Open Source in general) ❤️





































![An all-white graph with the x and y axis defined on the range [0, 1].](/matplotlib/codeswitching-visualization/fig1.png)